Polarization-Sensitive Coherent Diffractive Imaging Using HHG

Abstract

High harmonic generation (HHG) from lasers have attractive properties for probing ultrafast dynamics at the nanoscale. The spectral range of high harmonics at the extreme-UV and soft-X-rays ($\lambda \sim$ 100 nm–1 nm, $\hbar \omega \sim$ 10 eV–1 keV) enables element specificity, the short wavelengths combined with high spatial coherence allows for imaging with nanometric spatial resolution, the extremely short pulse durations provide access to dynamics faster than a femtosecond ($1 \ fs = 10^{-15}$ s), and all that, on a compact system. In this chapter, we focus on experimental aspects of imaging with high harmonics. First, we present the experimental system and the image reconstruction procedure. Second, we show experimental results from the various configurations that were used throughout this project. Finally, we discuss mechanisms that played an important role in this imaging effort, and would contribute to the advancement of nanoscale imaging.

1 Experimental Setup

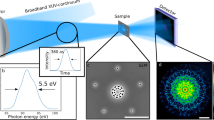
The experimental setup for high harmonic generation is schematically depicted in Fig. 18.1. The laser system delivers up to 8 mJ per pulse (pulse duration of 40 fs) at 1 kHz repetition rate, operating at a central wavelength of 800 nm. Initially, only a fraction of the output power of the laser system was used (between 0.4 and 1 mJ) for the generation of high harmonics in argon. Focusing the laser beam using a lens with a relatively short focal length of 20 cm ensures that the field intensity is sufficient to drive this nonlinear process. A typical Ar pressure needed for efficient harmonic up-conversion is more than 30 mbar. However, already at this pressure, most of the harmonics yield will be reabsorbed within a just a few mm. To mitigate the reabsorbtion of the generated radiation the interaction region is confined within a metallic capillary (diameter of 5–10 mm) with a very small entrance and exit holes that are self-drilled by the laser. Having only small holes is beneficiary, since it reduces the overall gas pressure in the generation chamber. Generally, the short absorption length of extreme-UV radiation requires that all experiments are carried out in high-vacuum conditions. After the HHG beam passes through an aluminum filter, a toroidal grating spatially disperses different harmonic orders, and refocuses a selected order onto the sample. When the sample is removed from the beam path all harmonic orders are incident on a charge-coupled device (CCD) camera and the HHG flux can be improved by finding the optimal phase matching conditions with a recursive fine-tuning of the following parameters: gas pressure, laser beam diameter, position of the capillary relative to the laser focus and the laser pulse chirp.

Fig. 18.1

Experimental setup for lensless imaging with high-harmonic radiation. Femtosecond laser pulses are focused in a gas cell filled with Ar or He. Generated harmonics are spatially dispersed with a toroidal diffraction grating and refocused onto a sample. The resulting diffraction patterns are recorded using a charge-coupled device camera. The measured spectra from Ar and He are shown on the left and on the right, respectively

The aluminum filter used in the experimental setup is a 150-nm-thick free-standing foil that separates the generation chamber and imaging system. It prevents oil contamination from the roughing pump of the generation chamber and blocks (by reflecting) any visible radiation, including the fundamental laser beam, from entering the imaging chamber. Depending on the thickness of the aluminum oxide layer, the transmission of the filter can be as high as 50% in the spectral range around 30 nm. The toroidal diffraction grating (550 grooves/mm, focal length 16 cm) spatially disperses the harmonics and refocuses them in its focal plane. In the used configuration the brightest harmonic order from Argon (23rd order, wavelength $\lambda$ = 34.8 nm) in the plateau region of the HHG spectrum is selected and isolated by the slit. The slit in front of the sample is used to reduce the unnecessary stray light in the imaging chamber.

The sample is positioned in the focus of the harmonic beam, and the light scattered off the sample forms a diffraction pattern which is recorded downstream at distances ranging from 15 mm to 60 mm with a cooled back-illuminated CCD-camera (20 $\upmu$m pixel size, 1340$\,\times \,$1300 array). When the CCD is placed closer to the sample, the scattered light is acquired at higher numerical aperture (NA) resulting to potentially higher spatial resolution. On the other hand, for the reconstruction procedure to converge, the diffraction pattern must be sufficiently oversampled [1], which requires to place the CCD far enough. In practice, the distance is chosen in a tradeoff between these two requirements.

The experimental results with quasi-binary mask samples are summarized in Fig. 18.2. The samples are prepared by focused ion beam (FIB) etching of silicon nitride membranes coated with a gold layer of different thickness: 150 nm (Fig. 18.2c, f), 200nm (Fig. 18.2b, e) and 460 nm (Fig. 18.2a, d). The left column shows the measured diffraction patterns on a logarithmic scale and the corresponding SEM micrographs of the samples in the insets. When recording at short distances, central spots of diffraction patterns can be overexposed after just a few seconds of exposure. Thus, to record high scattering angles (carrying high spatial resolution information) with sufficient signal-to-noise ratio (SNR) and to increase the dynamical range of the data, several identical diffraction patterns (5–100) of the same sample were captured and averaged. The diffraction patterns are not centro-symmetric, indicating a non-trivial phase-structure of the exit wave. To obtain (reconstruct) real-space images of the samples from the corresponding far-field diffraction patterns methods for coherent diffractive imaging (CDI) were implemented. The approach retrieves scattering phases from measured diffraction intensities. Further general information on phase retrieval can be found in Chap. 6. The magnitudes of the CDI reconstructions, i.e., the amplitude of light field distribution at the exit-surface of the sample are shown in the right column of Fig. 18.2 (in inverse gray colormap).

Fig. 18.2

Coherent diffractive imaging results using an illumination wavelength of 35 nm for various samples. Left column a–c—the measured diffraction data. Right column d–f—CDI reconstructions from the corresponding diffraction pattern. The scale bars of the reconstructions are 1 $\upmu$m, and the corresponding SEM images are placed as insets

To investigate the capabilities of lensless imaging with a high-harmonic source we designed various samples with different spatial features. These ranged from a heavily sparse objects (Fig. 18.2b, e) to a structure with a large open area (Fig. 18.2c, f). The diffraction pattern from the latter case requires an extremely high dynamic range since the central spot (mainly direct, unscattered beam) is very intense compared to the high-scattering angle components. This adds complexity to the data acquisition procedure, and typically requires a physical beam stop to block the intense center and consequent stitching of diffraction patterns captured with and without a beam stop. Furthermore, the phase retrieval process in the case of non-sparse object becomes rather challenging, as discussed next.

2 Phase Retrieval of Experimental Data

With the available detectors only far-field intensities can be recorded, while the phase information is lost. As discussed in Chap. 5, without this information one can back propagate the measured far-field data from reciprocal to real space using, e.g., Kirchhoff’s diffraction formula. Once the recorded far-field intensities are phased, the near-field information is linked by a Fourier transformation in the case of far-field diffraction. The missing-phase problem (see Chap. 5) can be solved with various well-established reconstruction algorithms for iterative phase retrieval described in Chap. 6 and [2, 3]. However, in realistic experimental conditions, the diffraction images must first undergo post-processing procedures. Furthermore, the real-space support, which is the necessary a priori knowledge, has to be defined. In our scheme, we used the same procedure for every sample, irrespective of its shape, to post-process diffraction data. The process has several steps: first, the dark counts (signal emerging from the camera itself, irrespective of the illumination) were removed by recording and subtracting an image without an HHG beam, i.e., a dark image. If necessary, the dark image was subtracted from the measured data with an additional constant offset. Second, the center of mass of each data set was used to center the diffraction patterns. Finally, the images were mapped onto an equidistantly-spaced discrete Fourier plane, i.e., the Ewald sphere, to account for distortions from the use of a flat detector [4, 5]. This correction becomes important at high numerical apertures.

To determine the support of the near-field, we start from the autocorrelation of the signal scattered form the object, that is, the Fourier transformation of the measured far-field intensities. A more precise support can be obtained by deconvolution of the autocorrelation function [6]. Depending on the shape of the sample, this deconvolved support can be sufficiently tight, and accurately define the transmissive parts of the object. Having a well-defined support drastically simplifies the phase-retrieval process. Generally, a subsequent refinement of the support can be achieved with methods such as “shrink wrap” [7] or by simply setting a magnitude threshold to the final reconstruction.

To examine the phase retrieval performance and to find the most suitable reconstruction algorithm for the data obtained experimentally, we applied and tested multiple algorithms: ER, DM, HIO, and RAAR, with some modifications for noise resistance [8, 9]. For HIO and RAAR with fixed relaxation $\beta$ parameter we added additional constraints and an averaging procedure since these methods do not tend to stagnate [10]. The reconstruction process was done for 2000 steps, after initiation from a random guess for the far-field phase. We notice that HIO and RAAR performed significantly better than the other algorithms, whereas ER fails to converge for most of the experimental data. To find successful reconstructions within a run of 2000 iterations for RAAR and HIO, the real space error (sum of counts outside the support) in every step is compared to the errors of the two preceding steps. Alternatively, one can calculate the far-field error by comparing the reconstructed far-field amplitudes with the measured data. If a local minimum of an error is found, the corresponding reconstruction is saved, with the purpose of keeping only ten reconstructions with the smallest error. Once all iterations are completed, the average of the 10 reconstructions corresponding to the 10 minima with lowest errors serve as the final reconstruction [10]. We note that averaging procedure was necessary only for data sets recorded with a relatively low SNR [11].

For the extended (autocorrelation-based) support, employing a positivity constraint in real space and limiting phase variations to less than $\pi$ was required for consistent convergence of the phase retrieval process. We found it useful to reconstruct an image multiple times, as described above, where a successful reconstruction provides for the tighter support for the next reconstruction procedure. This new support is determined as the reconstructed amplitudes above a certain threshold. A tighter support accelerates and improves the convergence, so the positivity constraint can be relaxed, or removed completely. Alternatively, in the shrink-wrap method [7], the autocorrelation-based support is repeatedly redefined during the first reconstruction run by shrinking the support to include only regions above some threshold every given number of steps. This technique, however, requires a few more fine-tune parameters, especially for non-sparse objects.

If the support is well-defined, we find RAAR (see Chap. 6, 6.25) to be the best method for reconstruction among the tested ones . Starting with a relaxation parameter, $\beta$ close to 1, we gradually reduced it down to 0.5 after the first few tens of steps. In this case, the algorithm converges consistently to a very similar or an identical solution every time, making a multi-image averaging redundant (see PRTF in Fig. 18.11 of Sect. 18.6) [10].

It is important to note that the above procedure was performed on diffraction data with linear oversampling of 4 and even lower without the need for a higher oversampling ratio to handle noise [12]. Increasing the oversampling ratio by recording at a larger distance, and/or by using a CCD with a smaller pixel size, and/or by imaging smaller samples adds information redundancy to the diffracion data, and thus, CDI becomes more noise tolerant. For the phase-retrieval imaging of smaller structures at a given resolution (inverse numerical aperture) has two additional advantages: It reduces the coherence requirements of the source [13, 14] as well as the dynamical range of the scattered signal. The reduced dynamical range is achieved since a smaller portion of the beam remain un-scattered, thus, saturation effects of the central spot of the diffraction pattern are less severe. For these reasons, the phase retrieval process of a diffraction pattern from a smaller sample may converge to a reasonable solution for the given parameters such as wavelength, CCD pixel size and NA even when the diffraction data have low SNR or insufficient bandwidth. In this regard, ptychography [15] can be, in many cases, an efficient approach. In ptychography, multiple diffraction patterns of the same object are recorded—one for every shift of a confined illumination. A large real-space overlap between the illuminated regions in each acquisition provides for additional redundancy in the data which eases the phase-retrieval process compared to a single diffraction pattern in CDI. Clearly this extra redundancy comes at a price of an increased exposure time, increased requirements for stability and positioning of sample relative to the beam.

The oversampling ratio is a pre-requirement for CDI, but the form of a sample may also drastically affect the phase-retrieval convergence. First of all, sparse objects have less data points with unknown values, i.e., number of pixels with values to be determined within the real-space support. Furthermore, a well-defined sparse object provides for an accurate autocorrelation support—a crucial step for a successful reconstruction. This further reduces the number of unknowns due to a tighter support and “forbids” the reconstruction to move within the support. An uncertainty in the position of the reconstruction within the support will lead to a blurred reconstructed image, especially when non-stagnating algorithm is used together with an averaging over multiple reconstructions. In this regard, an object with a cross-correlation term with a delta function (single pixel, or close to that) in the autocorrelation (inverse Fourier transformation of the measured far-field intensitites) gives a significant improvement for the phase retrieval. This feature is demonstrated in Sect. 18.5 with small holographic reference holes drilled in the vicinity of an investigated specimen.

The parameters discussed above also affect the number of steps required for phase retrieval. For instance, in similar experimental conditions, a reconstruction based on RAAR algorithm was accurate after just over 50 steps, (Fig. 18.2b, e data in Sect. 18.5), or required hundreds to thousands of iterations (Fig. 18.2a, c, d, f).

3 Experimental Results

The reconstructions in Fig. 18.2 are in a good agreement with the SEM micrographs. However, further inspection of the experimental results reveals field and phase modulations that, at a first glance, may not be expected from a binary opaque transmission mask. Interestingly, such modulations have not been identified or reported in the literature even for a very similar experimental conditions. This might be because the achieved spatial resolution was not sufficient to accurately resolve such small features. In this case, the interpretation of the experimental results as well as an estimate for the achieved spatial resolution might be misleading. In the follwoing we show that the origin of these modulations is associated with the light propagation and multiple scattering within the objet (in this case opaque binary mask) itself.

The reconstructed field—the field profile at the sample’s exit surface—relates to a product of the incident field profile and a non-scalar transmission function of the object. While Si$_3$N$_4$ as well as gold are optically thick media at extreme-UV wavelengths, the light propagating through the removed regions of the sample can be represented as a sum of discrete propagating eigen modes, equivalent to the propagation of electromagnetic wave in a waveguide. These modes propagate through the sample to its exit surface, where they scatter and freely travel to the detector. Clearly, the exit-surface wave is a superposition of these propagating modes and the observed modulation in the reconstructed image resutls from multi-mode interference. In the following, we perform 2D and 3D numerical simulations using finite element modeling and semi-analytical solution to corroborate the experimental findings.

Fig. 18.3

Interpretation of the experimental results: waveguiding at extreme-UV. a Numerical simulations of light propagation in slab waveguides for the wavelengths and materials used in the experiment. The waveguide dimensions correspond to the regions of the sample marked with L1, L2 and L3 in (a) and C1, C2 and C3 in (c). Solid blue lines—measured data, red dashed lines—simulated data. b Three dimensional simulation of light propagation in rectangular waveguides of various sizes with our experimental conditions

Figure 18.3a shows a 2D numerical simulation of light propagation through slab waveguides of different width with geometries similar to the experimental conditions (marked with three solid lines L1–L3 in Fig. 18.2d). The material properties and wavelengths are as in the experiment as well. The field distributions at the exit surface of the waveguides are plotted with red dashed lines for numerically simulated data in the right column of Fig. 18.3a. The solid blue lines depict the experimental field values obtained from lineouts L1–L3 in CDI reconstruction. Similarly, the structure marked with a red dashed rectangle in Fig. 18.2f can be approximated as 2D slab waveguides of different width and the expected exit surface field distribution can be simulated. The blue solid lines and the red dashed lines in the bottom of Fig. 18.3c are the experimental and simulated lineouts for the regions marked as C1, C2 and C3. For the structure shown in Fig. 18.3b, e, aspect ratios of individual features (waveguides) are not as high as in the case of the structures shown in Fig. 18.2d, f. Therefore, here the approximation of the structure with a 2D model as a slab waveguide is not accurate and a 3D simulation is required. Figure 18.3b compares the expected exit surface fields (simulated using a 3D finite-element modeling) on the left with the experimentally measured ones on the right (from reconstruction shown in Fig. 18.2e) for two different waveguides. Again, as in the case with the other samples the reconstructed field distribution is in a close agreement with the simulated data.

Fig. 18.4

Analytical solution for waveguiding for interpretation of the experimental results shown in Fig. 18.3. a Field profiles of first three allowed eigenmodes in a symmetrical slab waveguide. b Mode transmission through 700-nm-long gold waveguide with perpendicular (TM) and parallel (TE) incident polarization

Fig. 18.5

Coherent diffractive imaging using illuminating wavelength of 30 (a, c) and 47 nm (b, d). The damping of higher order modes is already evident from the far-field diffraction patterns which is accurately reproduced in CDI reconstructions

Further insights into waveguiding at extreme-UV frequencies and fundamental reasons for mode beating at the exit surface of CDI reconstructions follow from a semi-analytical solution of the mode propagation within the structure using eigenmode expansion. Figure 18.4a demonstrates field distribution (field profile) of the first three eigenmodes in a gold-cladded slab waveguide. Figure 18.4b shows the computed transmission of these modes through a 700-nm-long waveguide as a function of waveguide’s width. Here, TE and TM modes correspond to the polarizations parallel and perpendicular to the cladding, respectively. We note that only even order modes are supported by a symmetrical waveguide. As expected, higher order modes experience stronger damping in narrow waveguides. Thus, the relative intensities of these modes at the exit surface are governed by the waveguide dimensions and the intensity profile resulting from a superposition of these modes at the waveguide’s exit can strongly differ for very similar geometries, e.g., a slight width difference.

Similarly, the illuminating wavelength affects the mode distribution at the exit plane. Figure 18.5 illustrates the experimental results of the same object imaged with a wavelength of 30 nm (a, c) and 47 nm (b, d). The zoomed regions (insets) emphasize the difference of the reconstructed fields. The image obtained with the longer wavelength contains dominantly the fundamental mode, whereas the image obtained with 30 nm wavelength exhibit a complex mode-beating profile. Notably, this feature is already evident from the corresponding diffraction patterns, where the maximum spatial frequency (spatial frequency with sufficient SNR) scattered off the sample at 47 nm wavelength is much lower than the ones present on Fig. 18.5a, recorded with 30 nm illuminating wavelength. High-order waveguiding modes for longer wavelength are strongly damped due to a multiple scattering within the object and do not pass through the structure to its exit surface and therefore absent (heavily suppressed) on the far-field image as well as on the reconstruction. Clearly, for such high aspect ratio structures or for the structures comparable to the illuminating wavelength the sharpness of the CDI reconstruction will be limited to the highest Eigen mode transmitted. Therefore, using a knife-edge technique without accounting for wave propagation effects in such structures might lead to a strong overestimation.

We note, however, that a similar mode-beating profile can be observed when the high spatial frequencies are not fully recorded in the far-field, i.e., span beyond the CCD edges. Such a truncation of the far-field intensities determines the upper limit for the spatial resolution of the reconstructed image.

Fig. 18.6

Adapted from [10]

Coherent diffractive imaging with high dynamic range data demonstrates influence of SNR ratio at high scattering angles to the reconstruction quality. Note that fine features of the wavegude mode beating pattern cannot be resolved from the non-HDR (top) diffraction data with low SNR ratio.

To obtain high spatial resolution one needs to collect data at high NA. However, in most cases the signal-to-noise ratio at high scattering angles might be very weak and this will limit the maximum spatial frequency that can be accurately reconstructed with a phase retrieval algorithm and consequently the achieved spatial resolution. This is demonstrated in Fig. 18.6 where two diffraction patterns of the same structure are recorded with the same wavelength (35 nm) and the same NA (0.5). The top row shows a single diffraction pattern recorded for 5 s and the corresponding reconstruction. The bottom row is an average of 200 individual exposures (HDR data), so the signal-to-noise ratio especially at high scattering angles (c.f. insets) is improved. The effect of higher SNR ratio also imprints to the corresponding CDI reconstruction demonstrating a sharper image. While both reconstructions are in a good agreement with the SEM micrographs, the second CDI reconstruction from HDR data contains finer features that cannot be resolved in the first reconstruction. This is because the diffraction signal from smaller features scatters at higher angles where SNR is noticeably lower. Increasing the dynamic range by multi-exposure averaging results in a better SNR at high scattering angles and improves spatial resolution, although both images were recorded at the same NA. Clearly, poor quality of a diffraction pattern and/or non-accurate phase retrieval impede imaging with high resolution irrespective of how high the NA is.

4 Polarization Dependence

Figure 18.4b shows a simulation of wave propagation within a gold-cladded waveguide. As discussed in Sect. 18.3 for a relatively narrow waveguide (smaller than 70 nm) higher-order modes can be fully damped whereas the fundamental mode may still be transmitted with relatively low losses. The narrower the slit the stronger the polarization anisotropy, i.e., transmission difference for polarization parallel (TE mode) and perpendicular (TM) to the walls of a waveguide. Higher suppression of the TM polarization can be explained by the fact that perpendicular fields penetrate deeper into the gold cladding where it experiences an exponential decay. Interestingly, this polarization dependent transmission effect is opposite to the one in wire-grid polarizers where perpendicular polarization is transmitted.

To investigate this phenomenon and its effects in nanoscale imaging with extreme-UV radiation, we designed and fabricated a structure with an angular arrangement of identical 50 nm-wide slits, etched in a gold coated Si$_3$N$_4$ membrane. The SEM image of the structure is shown in Fig. 18.7a. The diffraction pattern shown in (Fig. 18.7b) was recorded with S-polarized illumination at wavelength of 35 nm. The corresponding CDI reconstruction (exit-field intensity) is shown in Fig. 18.7c. The reconstruction reveals that slits parallel to the field polarization appear noticeably brighter than the ones that are perpendicular to the electric field. Figure 18.7d plots the field intensity transmitted through each slit as a function of the angle between the slit orientation and the polarization, with comparison to Malus’ law for an imperfect polarizer. The reconstructed field (red circles) and the measured angular far-field (blue triangles) accurately follow the predicted pattern. The measurement was done for multiple linear-polarization states to verify that the polarization dependence originates solely from the sample, and that the slits are indeed identical. In contrast to far-field pattern where it is impossible to disentangle contributions from parallel slits, intensity information from the reconstructed image provide information for each slit individually. Based on the quantitative information from the CDI reconstruction and the simulated polarization dependence for such a structure, we estimated width of the slits to be 52 nm.

Fig. 18.7

Extreme-UV polarimetry. a An SEM image of a structure with nanoscale slits. The width of the slits is identical. b The diffraction pattern in logarithmic scale. c The reconstructed intensity at the exit surface of the sample obtained by CDI from (b). d An analysis of the experimental data showing polarization dependent transmission through the nanoscale slits. Experimental data from the CDI reconstruction and from the diffraction pattern (red circles, and blue triangles, respectively). The line is the Malus’ law for an imperfect polarizer

Fig. 18.8

Polarizer for Extreme-UV radiation. a An SEM image of the structure with nanoscale slits of a typical width of 40 nm. The structure demonstrates polarization dependent transmission with high extinction ratio ${}^{TE}\!/_{TM}$ mode

This experiment brought three insights to Lensless imaging with a high-harmonic source:

• 1. In the extreme-UV and soft-X-ray range the scalar projection approximation is not valid. Instead, CDI can be used to accurately and quantitatively map polarization anisotropies and waveguiding effects at nanoscales.

• 2. A structure with nanoscale slit arrangement provides information on the polarization state of the incident extreme-UV light in a single acquisition measurement compared to a conventional reflection-based polarimeter, where incident polarization can be estimated only from a series of measurements at various angles [16]. This polarization analyzer shown in Fig. 18.7a proved to be very useful in the future experiments where optimization of polarization state of the extreme-UV light was required.

• 3. A structure with an array of only parallel nanoscale slits can serve as an effective polarizer for extreme-UV radiation as demonstrated in Fig. 18.8. Here, the diffraction patterns contain detectible scattering signal only from the polarization component parallel to the slits. The verification of the polarization anisotropy was done by rotating the sample and rotating the incident polarization.

5 Magneto-Optical Imaging Using High-Harmonic Radiation

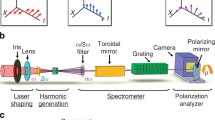
Recent developments in the generation of high harmonics with arbitrary polarization [17, 18] allows to access X-ray magnetic circular dichroism (XMCD). The M-edge absorption lines in the important 3d-ferromagnets Fe (52 eV), Co (60 eV) and Ni (75 eV) are within the spectral range of a typical HHG source based on a Ti:Sapphire amplified laser [19, 20], and additional materials (e.g. Gd, 145 eV) can be accessed using HHG sources at the soft-X-ray [21]. The circularly polarized HHG are generated by a bi-chromatic laser field in a gas (typically He). The laser field combines the fundamental laser and its second harmonic $\lambda =800$ nm and $\lambda =400$ nm, respectively. The driving fields are circularly polarized, with opposing handedness, thus the selection rule for the high harmonics imposes the suppression of every third harmonic order, while the allowed harmonics are circularly polarized [17, 22]. In this project, we implemented two schemes for circularly polarized high harmonic generation, as described in [17, 18]. We find that the latter scheme, namely an in-line MAZEL-TOV (stands for MAch-ZEhnder-Less for Threefold Optical Virgina spiderwort) device, is robust and reliable, due to its inherent transmission geometry. This device offers a drastically simplified alignment process compared to the scheme involving a Mach-Zehnder interferometer. The use of a single quarter-wave retarder to set the polarization of the bi-chromatic field enables a direct control on the laser polarization in the gas, and therefore, on the HHG polarization. For example, a reflection from a tilted surface may result in an unequal amplitude or phase for the incident TE or TM polarizations, thus deteriorating the laser’s degree of circular polarization. For the detection of XMCD contrast a direct polarization control is crucial—the helicity of the circularly polarized HHG is flipped from left-handed to right-handed by flipping the quarter-wave plate (QWP) retarder to $45^\circ$ or to $-45^\circ$. Furthermore, the MAZEL-TOV apparatus enables a straightforward fine-tuning of the recollision process in a way that allows to access to any harmonic order with circular polarization, even including the typically-suppressed harmonics orders (e.g. $36,39,\ldots$) [23].

Fig. 18.9

Experimental setup for nanoscale magnetic imaging using high-harmonic radiation. a A scheme of the experiment, b A measured spectrum generated using a circularly polarized bi-chromatic field tailored with MAZEL-TOV device. The suppression of every third harmonic order (e.g. $\ldots , 30, 33, 36,\ldots$) indicates that the harmonics are circularly polarized. The toroidal grating focuses the harmonics on the sample plane, and a slit selects the 38th harmonic order (59 eV), which provides for the optimal XMCD contrast in Co. To isolate the magneto-optical signal, two diffraction patterns are recorded—one with left- and one with right-handed circularly polarizated HHG beam. The sample includes the region of interest (central aperture) and four fully-drilled reference holes provide for a strong reference field that interferes in the far-field with the scattering from the magnetic sample

The experimental scheme for magnetic imaging with high harmonics is depicted in Fig. 18.9. The HHG source is based on the setup described in Sect. 18.3, with some modifications [20, 24]. First, Ar gas was replaced with He, which has a higher ionization potential and, thus, generates higher harmonic orders [25]. Specifically, we can access the 38th harmonic order in He and in Ne, providing for the optimal XMCD contrast at the M-edge of cobalt [26]. Helium was preferred over neon, since the price is significantly lower and the smaller absorption coefficient may results in brighter harmonics with a better beam quality. However the pulse energy (2–3.5 mJ) required to drive HHG process in He is higher than for Ar due to a higher ionization potential and higher phase matching pressures. Second, the need for circularly polarized HHG required the use of a MAZEL-TOV device. This device is inserted after the focusing lens to convert the linearly-polarized driving laser field into a bi-chromatic counter-rotating field. Finally, the interaction region, i.e., the focus of the fundamental beam, was positioned further away from the diffraction grating. This allowed us to illuminate a larger number of slits on the grating, which improves the spectral dispersion of the toroidal grating. Increasing the dispersion improved the temporal coherence of the beam in the sample region, and thus allows for a higher spatial resolution [1]. We note that, for previous experiments, described in Sect. 18.3 the estimated monochromaticity ${}^{\lambda }\!/_{\varDelta \lambda }$ was larger than 500, corresponding to a spatial resolution down to $\sim$30 nm [1, 12]. For the magneto-optical imaging experiments, the monochromaticity was increased to enable improved resolution—beyond 20 nm. In a more recent development, the sample was illuminated with a replica of the fundamental beam ($\lambda =800$ nm), through a controlled time delay with respect to the HHG beam. This pump-probe addition would allow to combine imaging experiments with femtosecond time resolution enabling movies of ultrafast magnetic dynamics at the nanoscale.

In order to isolate a magnetic signal from non-magnetic background, two diffraction patterns with opposite helicities were recorded (c.f. L and R in Figs. 18.9 and 18.10 for the illumination with left- and right-handed circularly polarized 38th harmonic, respectively). The HHG helicity (L vs. R) is easily done by rotating the quarter wave-plate of the MAZEL-TOV device from $45^\circ$ to $-45^\circ$, and vice versa. For each helicity, the diffraction pattern dynamic range was increased by combining two exposure times. A long exposure—up to 10 min per helicity—provided the diffraction pattern for the medium and high scattering angles with sufficient SNR. A short exposure time (typically several images of a few seconds each) captured the low scattering angles, without any saturation effects. For example, diffraction patterns shown in Fig. 18.10a are composed of scattering data from an exposure time of 10 min with the average of 24 frames of 5 s exposure each. The diffraction patterns were scaled properly and stitched to form a single diffraction pattern with high dynamic range. Finally, the diffraction patterns were prepared for reconstruction as described in Sect. 18.1.

Fig. 18.10

Lensless imaging of nanoscale magnetic domains using high-harmonic radiation. a Holographic diffraction patterns recorded with left- (L) and right-handed (R) circularly polarized 38th harmonic order. b A full-field Fourier transform holography (FTH) reconstruction. c The magneto-optical absorption (top) and phase contrast (bottom) reconstructions as recovered with FTH. The spatial resolution is estimated between 150 nm and 200 nm. d the magneto-optical absorption and phase contrast, as reconstructed via CDI. Using CDI, the spatial resolution reaches below 50 nm

The phase retrieval process used for the magneto-optical images is similar to the one described in Sect. 18.2. As the real-space support, a single cross-correlation of the diffraction pattern was used. Since for magneto-optical experiments we used reference holes, the cross-correlation includes accurate replicas of the structure, and thus dramatically improves the convergence of the phase retrieval algorithm. For samples with reference holes, the required number of RAAR steps can be reduced to about a 100. The combination of FTH with CDI allows for a direct low-resolution but noise-tolerant reconstruction by a single-step Fourier transformation, and a high resolution CDI reconstruction. The experimental results from the magnetic structures are summarized in Fig. 18.10. First, two diffraction patterns from left- and right-handed circularly polarized illumination are recorded (c.f. L and R in (a), shown in logarithmic scale). Second, a single Fourier transformation of the measured far-field intensities provides for the holographic reconstruction (Fourier transform holography—FTH). Finally, the real-space support is derived from the FTH, thus assisting the iterative phase retrieval to recover the high resolution image. Figure 18.10b shows the magneto-optical amplitude for the holographic reconstructions. Since the sample had four reference holes, the FTH reconstructs eight replicas of the sample—a reconstruction and its complex conjugate for each reference hole. The magneto-optical amplitude (top) and phase (bottom) contrasts originating from the smallest reference hole (approx. 200 nm in diameter) are shown in Fig. 18.10c. The magnetic phase contrast is the phase difference between the reconstructions recorded with left- and right-handed HHG helicity. The corresponding magneto-optical contrast CDI reconstructions based on the RAAR algorithm are shown in Fig. 18.10d. Both the FTH and the CDI reconstructions show the same pattern of magnetic domains. The resolution of the CDI reconstruction is clearly higher (below 50 nm), since it is limited by the high NA recorded far-field, whereas, the resolution of the FTH reconstruction is set by the pre-drilled reference hole. Notably, the CDI reconstruction in this case has a multiple binary-like transitions between up and down magnetization, where the domain transition region is below a single-pixel in a vast region of the image. Since the domain-wall width for this Co/Pd multilayer structure is expected to be 10 nm to 15 nm, it can provide for a test sample for higher resolution imaging, even below the illuminating wavelength ($\lambda _{38{\text {th}}\,\text {harmonic}}$ = 21 nm) to investigate the capabilities of HHG for magnetic imaging.

In principle, the size of reference holes can be reduced in order to improve the spatial resolution of the Fourier-transform hologram. However, the intensity of the light transmitted through a small reference hole is significantly lower due to propagation effects in the narrow channel (see Sect. 18.3). As a result, longer exposure times would be required. Additionally, the manufacturing of narrow reference holes is a technical challenge, limiting the repeatability of the experiment. A convenient approach in FTH is to use of reference holes of slightly varying sizes. Thus, the achievable spatial resolution (hole size) and an image contrast (hole transmission) can be determined while analyzing the scattering data. In a later section we show that adding large and strongly scattering reference holes to the sample, assists the CDI reconstruction in few ways [20]. First, determining the support from the cross-correlation is much easier and the phase retrieval algorithm converges faster when reference holes are introduced. Second, the interference of weak scattering signals with a strong reference field enhances the weak signal so that it can be detected above the instrumental noise level [27, 28]. In contrast to FTH, the size of reference holes plays a secondary role in determination of resolution in CDI experiments. To demonstrate this, we designed a similar structure with reference holes larger than the sizes of the features to be observed.

Fig. 18.11

Magnetic imaging using large reference holes. a Holographic diffraction pattern recorded with left-handed circularly polarized light. Inset highlights very good speckle visibility at high scattering angles. b CDI reconstruction of (a) for a single helicity illumination. Image contains magnetic as well as non-magnetic contributions. c Magnetic phase-contrast CDI reconstruction, i.e., isolated XMCD signal. d PRTF for 20 reconstructions initiated from a random first guess indicating a consistent convergence for all spatial frequencies recorded. e Exit fields of the reference holes (interpolated) demonstrating strong intensity modulations due to waveguidng and Fourier-truncation effects

Figure 18.11 shows the imaging of worm-like domains in a Co/Pd multilayer stack in a field of view diameter of 4 $\upmu$m, for which the reference holes in the mask had a diameter of 500–600 nm. These diameters are twice larger than a typical size of the magnetic-domains and an order of magnitude larger than the final resolution for images obtained via CDI reconstructions. Figure 18.11a shows the diffraction pattern recorded with left-handed circular polarization and Fig. 18.11b shows the field magnitude of the corresponding CDI reconstruction. Note that the image is presented with a true-pixel resolution and contain features in the order of a single pixel. Figure 18.11c represents the phase contrast dichroic image, which is the angle of the ratio of two reconstructions recorded with opposite helicities. Despite the fact that reference holes are too large to resolve individual magnetic domains via FTH, CDI successfully retrieves high-resolution information by finding the far-field phase at high NA. To estimate the achieved spatial resolution, we use the phase retrieval transfer function (PRTF) [29] . Here, PRTF is calculated as the average far-field phase of 20 reconstructions that were initiated from a random first guess phase. Figure 18.11d depicts that the phase retrieval process is consistent throughout the entire far-field. Reconstructed phase reaching beyond 15 inverse $\upmu$m corresponds to a spatial resolution better than 33 nm. However, since the truncation of the diffraction patterns at the physical edges of the CCD begins just above 10 $\upmu$m, the spatial resolution that can be claimed is defined by this value to 50 nm (a single pixel resolution).

6 Dichroic Imaging

The extrme-UV light propagating in the reference holes undergoes the same waveguiding effects, as described in Sect. 18.3 (c.f. Fig. 18.11e). A similar effect is noted near the edges of the central aperture (c.f. Fig.  18.11d). Generally, wave effects in the illuminating field reduce the image quality and add artefacts [11] that are associated solely with an imaging scheme (a Fresnel number for the used wavelength and sample geometry). In contrast, dichroic imaging provides for a unique type of microscopy, which can eliminate these effects in the reconstructed image. When the magnetization map is obtained from the ratio of two reconstructed images with opposite helicities (L and R helicities), the artifacts vanish. The dichroic contrast isolates the magnetic (dichroic) signal from the non-magnetic background.

Fig. 18.12

Waveguiding and edge-diffraction artifacts elimination with dichroic imaging. Left and middle images are absorption contrast reconstructions for left (L) and right (R)-handed circularly polarized illumination. Wave modulations from edge diffraction effects are observed and can not be separated from magnetic signal. Right image—a dichroic image—the ratio of L/R isolates the magnetic signal from non-magnetic contributions

Figure 18.12 shows a part (left lower quarter) of the central aperture for left- and for right-handed circularly polarized illumination marked as L and R. The image for each helicity exhibits fine intensity modulations in the order of a single pixel, mainly near the edge of the aperture. These fine modulations are real but cancel each other out in the dichroic image (Right image in Fig. 18.12 for the ratio L/R), provided that reconstructions from opposite helicities are accurately overlaid. To consistently position the two reconstructions with a sub-pixel accuracy, it is convenient to match the lower order moments of their far-field phase (i.e. the global phase, and the phase gradients). To do so, we fully reconstruct the data recorded for one helicity, and use its far-field phase as an initial guess for the phase retrieval of the opposite helicity diffraction pattern. Since the dichroic component is only a small component of the far-field, only a few iterations are required for a full phase retrieval, when starting from the far-field phase of the opposing helicity. This provides for a robust and reliable imaging of magnetic samples without any artifacts of smearing effects from reconstruction shifts and waveguiding effects.

Fig. 18.13

Signal enhancement effect through the interference with a strong reference wave. (left) A diffraction pattern from a sample with very narrow reference holes (sub-100 nm). (right) A diffraction pattern from the same sample with large reference holes (500–600 nm). The larger reference holes result in a high signal-to-noise ratio at higher scattering angles. The weak magneto-optical signal scales as square-root of the strong reference intensity, because it is an interference effect. Since the reference holes allow for the auxiliary field to cover the entire CCD, the weak signal is amplified above the noise throughout the recorded diffraction pattern, and a high-resolution image is reconstructable

7 Signal Enhancement Mechanism

A strong reference or an auxiliary wave in the vicinity of the field-of-view has an advantage for recording diffraction data. Specifically, a strong scattering field from multiple reference holes interferes on the CCD detector with the weak magneto-optical scattering signal. Thus, photons carrying magnetic information can be detected above the instrumental noise, and the exposure times can be drastically reduced. Figure 18.13 shows a comparison of two diffraction patterns recorded from the same structure, albeit with a different intensity of the reference field. When the reference holes were small (left), the signal includes mostly the low-angle scattering from the central aperture, where the high resolution information is buried and lost in the noise. When the reference holes are large (right), a meaningful portion of the light passes them and scatters to higher angles, thus lifting the signal above the level of the instrumental noise of the camera. Thus, this auxiliary field brings the weak magneto-optical scattering above the noise through interference. In this example, the scattering from the waveguides is two orders of magnitude higher when the reference holes are large, which means that through interference, the magneto-optical signal is enhanced by at almost one order of magnitude.